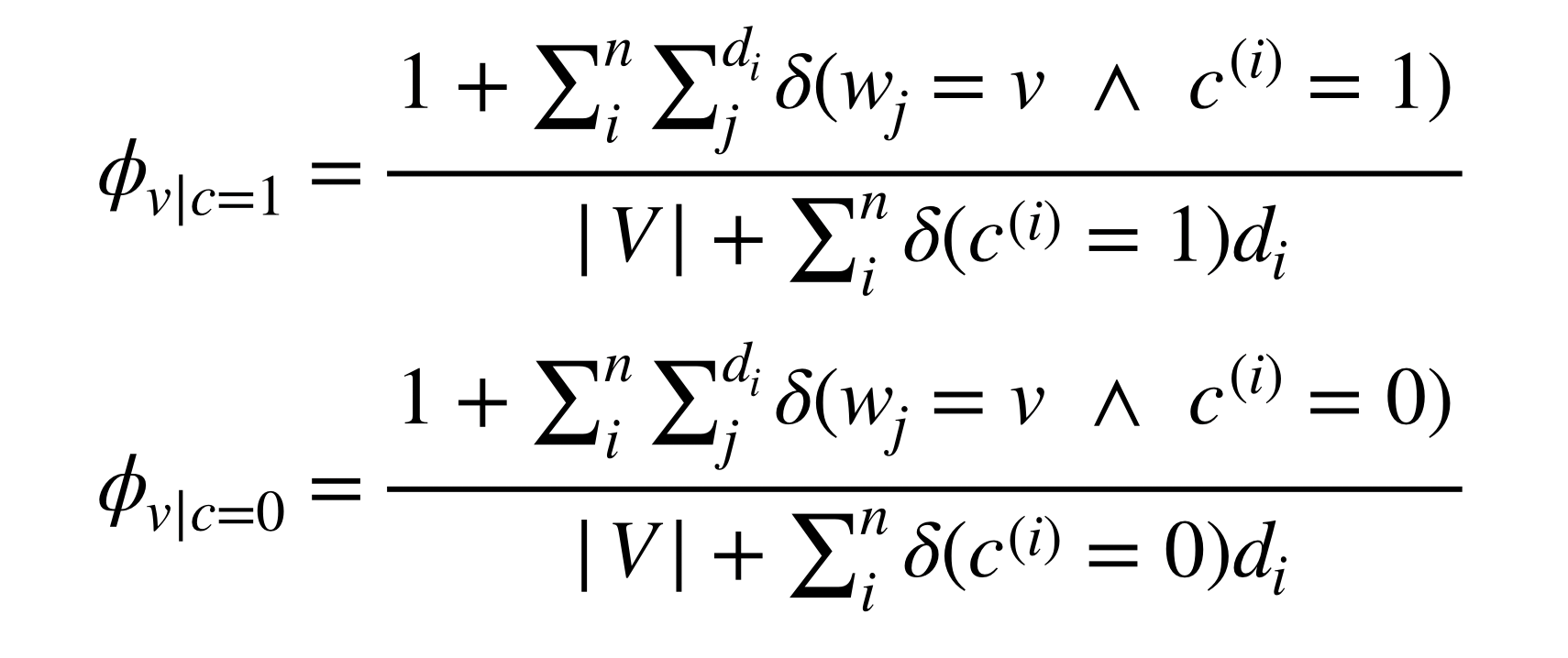[mathjax]
ナイーブベイズは文書データの分類に用いられる手法で、単純な理論ながら高いパフォーマンスを誇ることで知られています。SEEDATAでは、現在もアップデートが進むこの手法について独自でアルゴリズムを研究開発を進めており、このページではナイーブベイズ(NB)の基本的な理論背景とイベントモデルについて説明していきます。
1. ナイーブベイズのメカニズム – Bernoulli Event Model
1.1 入力となるデータ
テキスト分類と呼ばれる広範な問題の一例として、メールのスパムフィルターを構築することを想定しましょう。ここでは、メッセージが迷惑な商用メールであるか、非スパムメールであるかによって分類します。トレーニングセットとして、スパムまたは非スパムとしてラベル付けされた一連のメールを用意し、これら1つ1つの電子メールを表すため以下のようなベクトルを用います。

辞書内の単語数に等しい長さの特徴ベクトルを介し、メールを表します。具体的には、電子メールに辞書の(v)番目の単語が含まれている場合、(w_v=1)とし、それ以外の場合(w_v = 0)を与えます。たとえば上記のベクトルは、当該の文書の中に「アサイン」「新規事業」といった単語を含んでおり、「明日」「詫び」などは一度も登場しないということを表しています。ナイーブベイズにおいて、このようにバイナリ値のベクトルで文章中の単語を表現する手法をBernoulli Event Model(ベルヌーイ・イベントモデル)と呼びます。
特徴ベクトルにエンコードされた単語のセットはボキャブラリと呼ばれ、(w)の次元は語彙のサイズに等しくなります。 こうして任意の文章をベクトルで表現することができたので、今度は生成モデルとして(p(w | c))を定式化しましょう。しかし、仮にボキャブラリとして10000語の単語を用いた場合、(w)を多項分布で明示的にモデル化する場合(2^{10000})の可能性が想定され、(2^{10000}-1)次元のパラメタベクトルが必要となってしまいます。このままではパラメーターが多すぎるため、使い物になりません。
1.2 Naive Bayes Assumption
以上のような問題を解消して(p(w | c))をモデル化するために、非常に強力な仮定を置くこととします。 (c)が与えられた場合、(w_i)は条件付き独立であると仮定します。この仮定はNaive Bayes Assumptionと呼ばれ、結果のアルゴリズムはナイーブベイズ分類器と呼ばれます。以降は(c = 1)の場合、スパムメールを意味するとします。
例えば「新規事業」が(w_{1539})、「生活者」が(w_{6415})に対応するとき、 (c = 1)である場合(w_{1539})の値は (w_{6415})の値に影響がないと考えます。つまり、あらかじめスパム・非スパムがわかっているとき、メールの中で「新規事業」という単語と「生活者」という単語が出現することは独立であると考えるのです。これは$$p(w_{1539} | c)= p(w_{1539} | c,w_{6415})$$と表式することができます。 注意として、この仮定は「(w_{1539})と(w_{6415})が独立しており、(p(w_{1539})= p(w_{1539} | w_{6415}))が成り立つ」ということを意味するのではありません。あくまで(w_{1539})と(w_{6415})は条件付きで独立しているということに留意しましょう。この仮定を用いると、例えばボキャブラリのサイズを(V=10000)として(p(w | c))は以下のように表すことができます。
(normalsize{
p(w_1,w_2,…,w_{10000} | c)\[1.0em] =p(w_1|c)p(w_2|c, w_1)p(w_3|c, w_1, w_2) · · · p(w_{10000}|c, w_1, . . . , w_{9999}) \[1.0em] =p(w_1|c)p(w_2|c)p(w_3|c) · · · p(w_{10000}|c) \[0.5em] =prod^V_{v=1}p(w_v|c) })
以上でモデルの設定は完了しました。それでは、上式でメールを分類する際にどのようなボキャブラリが適切なのか考えてみましょう。
1.3 ボキャブラリーの構成、特徴量選択のための工夫
ここまでの議論で、分類器の性能向上のためにはボキャブラリーについて以下のようなポイントを押さえる必要があると考えられます。
1. 分類にクリティカルに効いてこない、一般的な単語を加えない
2. サンプル数が少ないときは、出現頻度の少ない単語をなるべく使わない
まず1について、仮にボキャブラリーに「お知らせ」という単語を加えたとします。当たり前ですが、スパムでも非スパムでも登場する可能性がある単語であり、フィルタとしては不適切な単語です。このように一般的な単語の追加は計算の時間を増大させ、非効率な分類器を作ってしまうことに繋がるため、避けなければいけません。
また2について、出現頻度が少ない単語は母集団の傾向に反した確率計算に繋がる可能性があります。例えば、全1000件のメールの中で「振込み」という単語が4件でしか出現しなかったとして、そのうち3件が非スパムであるとします。すると振込みという単語が出てきたとき、非スパムでない確率がスパムより3倍も高くなりますが、出現回数が4回では根拠として弱いと考えられます。というのも、もしサンプルを10倍にして10000件のニュースで同じ処理をした時、「振込み」はスパムメールの方が多く出現する可能性があるためです。

無論、これは1000件のサンプルが母集団の傾向を反映していない偏ったデータであったため、学習データを増やしていけば解決する問題ではありますが、実際ナイーブベイズを運用する際にはデータ数に制約があることもあり、注意が必要な点であります。このような問題を意識しながら、あらかじめスパム判別を行なったトレーニング用のメール集合を元に、単語ごとの出現確率を計算していきます。
1.4 出現確率を決定するための最尤推定
上記のモデルがワークするためには、以下の3種類のパラメタが必要になります。
・( phi_{v|c=1}= p(w_v = 1|c = 1)):スパムメールであるとき、単語(v)が出現する確率
・( phi_{v|c=0}= p(w_v = 1|c = 0)):スパムメールでないとき、単語(v)が出現する確率
・( phi_{c=1}= p(c = 1)):ある文書がスパムメールである確率
トレーニング用データとして、スパム・非スパムのラベルをすでに与えた(n)個のメール({(w^{(i)},c^{(i)});i = 1, . . . , n})を用意します。すると全データに対する尤度は以下のようになります。
$$L(phi_{v|c=1},phi_{v|c=0},phi_{c=1})=prod^{n}_ip(w^{(i)},c^{(i)})$$
(phi_{v|c=1},phi_{v|c=0},phi_{c=1})に関して(L)を最大化すると、最尤推定値が得られます。(N(cdot))を、条件を満たすメールの総数だとするとこれらのパラメタは以下のように表されます。
$$phi_{v|c=1}=frac{N(w_v=1 and c=1)}{N(c=1)}\[1.5em]
phi_{v|c=0}=frac{N(w_v=1 and c=0)}{N(c=0)}\[1.5em]
phi_{c=1}=frac{N(c=1)}{n}$$
それぞれのパラメタは、サイコロの目のようにとてもシンプルに計算されることがわかりました。ここからベイズの定理に基づいて、新たな文書データについて特徴量ベクトル(w^*)を用いてスパムメールである確率(p(c=1|w^*))を求めてみましょう。
(
normalsize{
p(c=1| w^*)
}\[1.0em]
large{
=frac{p(w^*|c=1)p(c=1)}{p( w^*)}\[1.0em]
}\[1.0em]
large{
=frac{big(prod_{v}^d p(w^*_v|c=1)big)p(c=1)}
{big(prod_{v}^d p(w^*_v|c=1)big)p(c=1)+big(prod_{v}^d p(w^*_v|c=0)big)p(c=0)}
}
)
ここまで、入力であるベクトル(w_v)がバイナリ値のみをとるBernoulli Event Modelを考えてきました。この手法は、主に短い文章からなる分類に有効とされています。しかし短い文書データや少ないデータセットを対象とすると、ゼロ頻度問題と呼ばれる現象が起こってしまうことがあります。
1.5 ゼロ頻度問題解決のためのSmoothing
ゼロ頻度問題とは、サンプルで出現していない単語をボキャブラリに追加した時発生する問題であり、この場合( phi_{v|c=1}= phi_{v|c=1}=0)となるため判別ができなくなってしまいます。そこで、先述のパラメタを以下のように置き直します。
$$phi_{v|c=1}=frac{alpha+N(w_v=1 and c=1)}{2alpha+N(c=1)}\[1.5em]
phi_{v|c=0}=frac{alpha+N(w_v=1 and c=0)}{2alpha+N(c=0)} (0leqalpha)$$
(alpha=1)の場合LaplaceSmoothing、(alpha<1)の場合Lidstone smoothingと呼ばれます。どちらの(phi)も(v)で和を取った時に1になっており、(phi)が0にならないように回避する形で変形されています。この場合でも、元の最尤推定量と同等の精度が保たれることが知られています。
2. 多項式に基づいたイベントモデル – Multinomial Event Model
これまでは、一つのメールの中で単語の出現をバイナリデータとして表現してきましたが、実際の文章では何度も登場する単語もあれば、1回しか出現しないレアな単語もあります。これらの回数も考慮に入れた手法が、Multinomial Event Model(多項分布モデル)です。
このモデルでは、先程まで0と1の二値しか取っていなかった(w_v)が、ボキャブラリのサイズを(|V|)として({1,2,…,|V|})の中からある正の整数値を取るようになり、一つのメールは((w_1,w_2,…,w_d))というベクトルで表されることになります。(d)は、メール内で出現したボキャブラリに属する単語の数で、メールによって異なる大きさを持ちます。例えばメールの書き始めが「新規事業について…」ならば(w_1=1539)というように、語順を保存してメールの単語を記録していきます。

多項分布イベントモデルでは、初めから順に単語が多項分布に従って発生し、(d)個の単語からなるメールを生成していると考えます。そこで、スパム・非スパムが明らかになった状態で、(v)番目の単語が(k)である確率(phi_{w_v=k|c=1},phi_{w_v=k|c=0})を用いることにします。さらに、(p(w|c))は同じ成分で順番の違うベクトル(w)に対して等しい確率を取ると仮定し、語順によらないBOWとしてモデルを構築してみましょう。これはちょうど、サイコロを振った時(3,6)の順で出るのと(6,3)の順で出る確率が同じで、一括りにして考えることと同じです。
トレーニングデータとして、スパム・非スパムが与えられ語順を保存した(n)個のメールを用いると、尤度関数は以下のようになります。
(
displaystyle
L(phi_{v|c=1},phi_{v|c=0},phi_{c=1}) = prod^{n}_ip(w^{(i)},c^{(i)})\[1.5em]
displaystyle = prod^{n}_i
big(
prod^{d_i}_v p(w_v^{(i)}|c;phi_{v|c=1},phi_{v|c=0})
big)
p(c^{(i)};phi_{c=1})
)
ここで、文書(i)はベクトル(w^{(i)}=(w^{(i)}_1,w^{(i)}_2,…,w^{(i)}_{d_i}))として表されています。尤度関数を最大化させ、先述のLaplaceSmoothingを用いると、最終的に3つのパラメタは以下のように求まります。
$$
phi_{v|c=1}=frac{1+sum_i^n sum_j^{d_i} delta(w_v=k and c^{(i)}=1)}{|V|+sum_i^n delta(c^{(i)}=1)d_i}\[1.5em]
phi_{v|c=0}=frac{1+sum_i^nsum_v^{d_i}delta(w_v=k and c^{(i)}=0)}{|V|+sum_i^n delta(c^{(i)}=0)d_i}\[1.5em]
phi_{c=1}=frac{N(c^{(i)}=1)}{n}
$$
ここで、( delta ( ) )は括弧内の条件が満たされた時に1を返し、それ以外は0となるデルタ関数です。(v)で和をとる事によって単語の順番が消去されていることがわかります。このように多項式イベントモデルの場合も単語ごとの条件つき確率を算出することができ、各文章について予測を立てることができます。
まとめ
ここまで、ベルヌーイ試行と多項分布に基づいた2種類のイベントモデルを見てきました。ベルヌーイ・イベントモデルはコインの裏表で単語の出現を決め、多項分布はサイコロで出現回数まで考慮していると言えるでしょう。しかし、ナイーブベイズはベイズと銘打ちながら、事前分布を仮定していないため完全なベイジアンではないという意見もあり、次回はその点について解説していきます。